I needed a custom memory allocator for use in the DPU software framework I designed as part of my thesis. The built-in C++ new was unacceptable because it used a best fit algorithm that runs in unbounded time. The result of this effort was a less sophisticated algorithm than the one presented here that allowed only two block sizes (one large, one small).
The algorithm I present here turns out to be very similar to the well-known McKusick-Karels allocator. The chief difference is that pages, not blocks, are placed into my primary linked lists and each page contains a linked list of its free blocks. The memory usage is essentially the same but additional operations are needed for allocations and deallocations. In exchange we get automatic coalescing and guaranteed constant-time operations.
Size of a page.
Minimum block size.
Number of entries in the Size array, and number of pages in the Page Array (see below). This value will generally be derived from the total amount of memory available for all data structures.
This is the memory that is being allocated. Blocks larger than PageSize can be handled by using a first-fit or best-fit algorithm to find contiguous pages of sufficient size. This possible extension is not considered here because such allocations cannot be performed in bounded time.
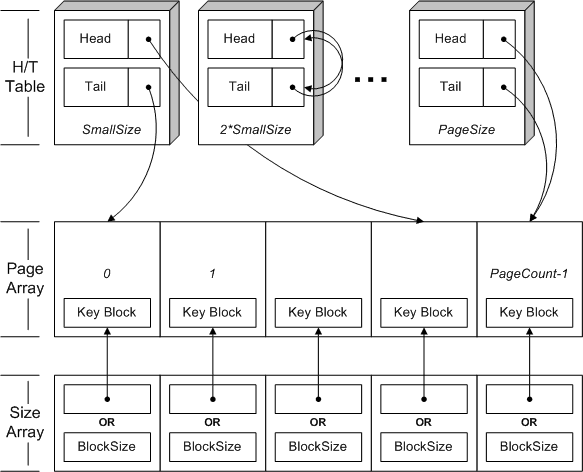
This is the list indicating which block size is being stored in a given page. Unlike the kmemsizes[] array used by the McKusick-Karels allocator, I store the log2 of the block size. Also, when a page is only partially full the Size Array entry will instead contain the offset to the Key Block (discussed below) and the Key Block will contain the block size. The data type stored in the Size Array is SizeType and will be no larger than a size_t in C/C++.
This is a list containing one head and one tail page index for each block size. There are log2( PageSize / SmallSize ) + 1 index pairs in the Head/Tail Table, and each index is a SizeType.
A number of additional variables, including the free page list head index and various pre-computed log2's, are stored in the class/struct instance of the allocator itself.

All free pages participate in a singly-linked list. A page index to the next free page is stored at the beginning of the first block of each page.
Each allocated page with at least one free block participates in a doubly-linked list according to its block size. One block (called the Key Block) contains the two page indices needed along with the block size, a singly-linked list pointer for the internal block list (see below), and a count of the number of blocks that have been allocated from this page. This places a minimum on the value of SmallSize.
Each Head/Tail Table entry contains the head and tail indices for a linked list of all pages of the corresponding size with at least one free block.
The Size Table entry corresponding to a page with allocated blocks is the log2 of the size of the allocated blocks being kept in that page. If all blocks in the page have been allocated, the entry contains the offset to the start of the Key Block instead. The entry corresponding to a free page is undefined.
Each allocated page with at least one free block contains an internal singly-linked list of all unallocated blocks that begins in the Key Block. The beginning of each free block other than the Key Block contains the offset to the beginning of the next free block. To maintain constant-time performance, a special end marker is available that means "all blocks after this one are also in the list". The blocks that follow in that page should be considered part of the linked-list even though they do not contain offsets to the next block.
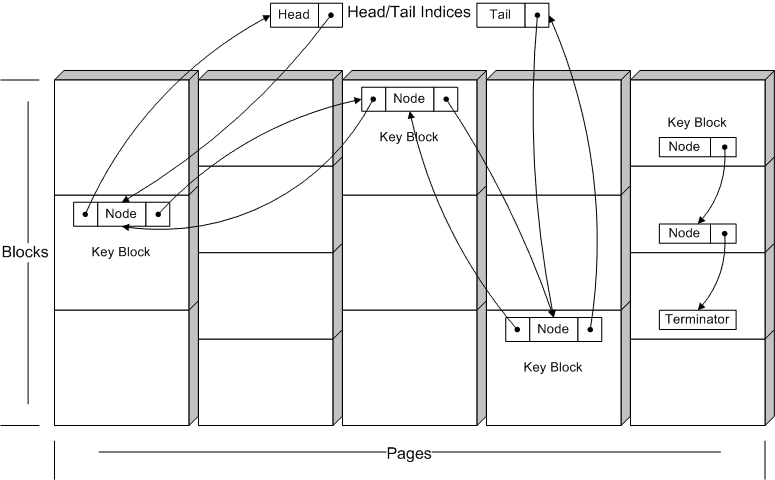
Marker value for end of singly-linked list of blocks.
Marker value for end of singly-linked list of blocks that implies all blocks that follow are included.
Allocation request in bytes.
Index into Head/Tail Table for Size, ranges 0 through log2( PageSize / SmallSize ).
Index of page in Size Array, ranges 0 through PageCount - 1.
Number of blocks per page for a given block size.
Offset of block relative to page start, ranges 0 through PageSize - 1.
Offset of the Key Block relative to page start.
Head of singly-linked list of free pages.
Use the size requested to find the appropriate Head/Tail Table list and move a page from the free page list to that list if that list is empty. Use the Size Array entry for the first page on that list to locate the Key Block. Check if the Key Block points to another block that we can hand out. If it doesn't, take the Key Block instead and remove the page from the list it was in. Return a pointer to the block we located.
| Input Size in bytes |
| SizeIndex is log2( Size ) - log2( SmallSize ) |
| If Head/Tail Table list for SizeIndex is empty, TakeFromFreeList( SizeIndex ) |
| Get PageIndex from front of Head/Tail Table list for SizeIndex |
| Get KeyBlockOffset from Size Array entry for PageIndex |
| Get BlockOffset from GetFreeBlock( SizeIndex, PageIndex, KeyBlockOffset ) |
| If BlockOffset = KeyBlockOffset, RemovePageFromFront( SizeIndex ) |
| Return pointer to block corresponding to PageIndex and BlockOffset |
| Input SizeIndex |
| Remove a page from front of singly-linked list that begins with FreePageIndex |
| Key Block is the first block of the page |
| Add page to front of doubly-linked Head/Tail Table list for SizeIndex |
| Set size element of Key Block to SizeIndex |
| Set allocated count element of Key Block to 0 |
| Set Size Array entry for page to point to Key Block |
| SecondBlock is SmallSize * ( 1 << SizeIndex ) |
| If SecondBlock = PageSize, set Key Block singly-linked list head to SENTINEL_END and return |
| Set Key Block singly-linked list head to SecondBlock |
| Set second block singly-linked list pointer to SENTINEL_CONT |
| Input SizeIndex, PageIndex, and KeyBlockOffset |
| BlockListHead is singly-linked list head in Key Block |
| If BlockListHead = SENTINEL_END, return KeyBlockOffset |
| BlockListNext is singly-linked list pointer in block pointed to by BlockListHead |
| If BlockListNext != SENTINEL_CONT, NewBlockListHead is BlockListNext |
| Otherwise, NewBlockListHead is ContinueBlock( SizeIndex, BlockListHead ) |
| Set singly-linked list head in Key Block to NewBlockListHead |
| Increment allocated count element of Key Block |
| Return BlockListHead |
| Input SizeIndex and BlockListHead |
| NextBlock is BlockListHead + SmallSize * ( 1 << SizeIndex ) |
| If NextBlock = PageSize, return SENTINEL_END |
| Set singly-linked list pointer in block pointed to by NextBlock to SENTINEL_CONT |
| Return NextBlock |
| Input SizeIndex |
| Remove page from front of doubly-linked Head/Tail Table list for SizeIndex |
| Set Size Array entry for page to SizeIndex |
| If Size is known at compile-time the log2 can also be computed at compile-time. Otherwise it will take O{ log2( bits in SizeType ) } basic operations to compute. |
| Total is an avoidable O{ log2( bits in SizeType ) } plus O{ 1 }. |
Use the pointer to be deallocated to find the page and block being deallocated. Look up the size of the page's blocks in the Size Table or in the Key Block it points to. If the size is in the Size Table, make the deallocated block the new Key Block and point the Size Table entry to it. Otherwise add the block to the front of the singly-linked block list in the Key Block and remove the page from the doubly-linked list it is in. Add the page to either the back of the appropriate Head/Tail Table list or the front of the free page list.
| Input Pointer to be deallocated |
| Get PageIndex and BlockOffset corresponding to Pointer |
| Examine Size Table entry corresponding to PageIndex |
| PageWasFull is true if the Size Table entry for PageIndex contains SizeIndex, false if it contains KeyBlockOffset |
| If PageWasFull, get SizeIndex from Size Table entry and MakeKeyBlock( SizeIndex, PageIndex, BlockOffset) |
| Otherwise get SizeIndex from size element of Key Block and RemovePageFromMiddle( SizeIndex, PageIndex ) |
| Decrement allocated count element of Key Block |
| If allocated count element of Key Block is 0, AddPageToFreeList( PageIndex ) |
| Otherwise AddPageToBack( SizeIndex, PageIndex ) |
| Input SizeIndex, PageIndex, and BlockOffset |
| Key Block is the block at BlockOffset |
| BlockCount is 1 << ( log2( PageSize / SmallSize ) - SizeIndex ) |
| Set Key Block singly-linked list head to SENTINEL_END |
| Set size element of Key Block to SizeIndex |
| Set allocated count element of Key Block to BlockCount |
| Set Size Array entry for page to point to Key Block |
| Input SizeIndex and PageIndex |
| Remove page at PageIndex from doubly-linked Head/Tail Table list for SizeIndex and repair list |
| Input PageIndex |
| Add page at PageIndex to front of singly-linked list that begins with FreePageIndex |
| Input SizeIndex and PageIndex |
| Add page at PageIndex to back of doubly-linked Head/Tail Table list for SizeIndex |
| Total is O{ 1 }. |
Use the pointer to be checked to find the page. Look up the size of the page's blocks in the Size Table or Key Block. Return the size.
| Input Pointer to be checked |
| Get PageIndex corresponding to Pointer |
| Examine Size Table entry corresponding to PageIndex |
| PageWasFull is true if the Size Table entry for PageIndex contains SizeIndex, false if it contains KeyBlockOffset |
| If PageWasFull, get SizeIndex from Size Table entry |
| Otherwise get SizeIndex from size element of Key Block |
| Return SmallSize * ( 1 << SizeIndex ) |
| Total is O{ 1 }. |
The table below compares the Hawkins allocator to the McKusick-Karels allocator with and without some form of coalescing. Note that McKusick-Karels can delay coalescing making it difficult to assign a cost to specific operations.
| Hawkins | M-K | M-K with coalescing | |
| Memory usage per page | 1 SizeType | 1 SizeType | 1 SizeType |
| Computing log2 for allocation | O{ log2( bits in SizeType ) } | O{ log2( bits in SizeType ) } | O{ log2( bits in SizeType ) } |
| Allocation worst-case | O{ 1 } | O{ 1 } | O{ BlockCount } |
| Allocation typical | O{ 1 } | O{ 1 } | O{ 1 } |
| Deallocation | O{ 1 } | O{ 1 } | depends on PageCount |
| Checking the size of a block | O{ 1 } | O{ 1 } | O{ 1 } |
| Constants in front of scaling | Generally larger | Generally smaller | Generally smaller |
| Coalesces? | Yes | No | Yes (may be delayed) |
Overall the McKusick-Karels allocator is likely to be more efficient than the Hawkins allocator in run-time performance, and may also offer additional space savings if the kmemsizes[] array is changed to store log2 of the block size (useful when the maximum block size is too large to fit in a byte). The primary advantages of the Hawkins allocator are:
In cases where coalescing is needed, the Hawkins allocator provides bounded operations suitable for use in real-time applications.
A fully-portable C++ implementation and a more constrained and efficient C implementation are in the works and will be posted under an open-source license when complete.
©2007 Donovan Hawkins <hawkins@cephira.com>
Cephira, Cephira.com, Cephira.org, Cephira.net, and CMPLT are unregistered trademarks of Donovan Hawkins